이야기에 앞서
이번 이야기는 문자열 검색 (String search) 입니다.
기본적인 개념은 주어진 문자열 (text)에서 특정 문자 (pattern)의 등장 위치를 찾는 것으로 문자열 검색, 문자열 탐색, String Matching 그리고 String Searching 등 다양한 이름으로 불리지만 모두 동일한 의미를 갖고 있습니다.
문자열 검색 알고리즘은 컴퓨터 과학에서 매우 중요한 주제 중 하나로 텍스트 에디터, 검색 엔진, 데이터 압축, 문자열 인코딩 등 다양한 분야에서 사용됩니다. 저희가 문서 작업에서 자주 사용하는 기능인 찾기 (CTRL+F)가 이러한 문자열 검색 알고리즘을 사용하는 대표적인 사례라고 볼 수 있죠.
이번 이야기에서는 가장 기본적인 방식의 Naïve 문자열 검색 알고리즘을 시작으로 보다 빠르고 효율적인 방식의 DFA와 KMP 알고리즘까지 차례대로 살펴보겠습니다.
문제 상황
문자열 $bananbanana$ 에서 $banana$를 찾아봅시다.
검색의 대상이자 주어진 문자열 ($bananbanana$)을 $T$ (Text) 그리고 찾고 싶은 문자 ($banana$)를 $P$ (Pattern)라 했을 때, 각 문자열의 특성을 다음과 같이 정의하겠습니다.
- $N$ : 텍스트 $T$의 길이
- $M$ : 패턴 $P$의 길이
- $\Sigma$ : 패턴 $P$에 등장하는 모든 문자(알파벳)의 집합
당연하게도 검색에 성공하기 위해선 패턴 $P$ 는 $T$ 의 부분 문자열이어야 하며, $T$의 길이인 $N$이 $P$ 의 길이 $M$ 보다 작을 경우 ($N < M$) 텍스트 내에 패턴이 포함될 수 없기 때문에 문자열 검색은 $N$이 $M$ 보다 크거나 같은 경우를 고려합니다. (typically $N \gg M$)
그럼 이제 패턴 $P$ $banana$ 가 텍스트 $T$ $bananbanana$ 내에 등장하는지 찾아보겠습니다.

눈으로 봐도 풀 수 있는 정말 쉬운 문제입니다.
첫 글자부터 차례차례 비교해보면 주어진 문자열의 6번째 위치에 있는 B 부터 끝까지 패턴 바나나🍌와 완벽하게 일치한다는 것을 알 수 있죠. 정리하자면 패턴 $P$는 텍스트 $T$ 내에 한 번 등장하며 그 위치는 6이라고 할 수 있습니다.
그렇다면 컴퓨터는 이 문제를 어떻게 풀 수 있을까요?
Naïve search algorithm
Naïve Search 알고리즘은 말 그대로 순박한 알고리즘 입니다.
반복문을 Nested 하게 사용하면서 주먹구구식으로 가능한 모든 위치에서 패턴의 등장 여부를 판단하기 때문에 Brute-Force 알고리즘이라고도 할 수 있죠.
List<Integer> naiveSearch(String text, String pattern) {
List<Integer> matched = new ArrayList<>();
int n = text.length();
int m = pattern.length();
for (int i = 0; i <= n - m; i++) {
int j = 0;
while (j < m && text.charAt(i + j) == pattern.charAt(j)) {
j++;
}
if (j == m) {
matched.add(i + 1);
}
}
return matched;
}
코드에서 볼 수 있듯이 naiveSearch() 함수는 문자열 $T$ 에 해당하는 ($\sum_{i=0}^{N-M}$) iteration 과 패턴 $P$ 에 대한 ($\sum_{j=0}^{M-1}$) iteration을 수행하면서 패턴의 등장 여부를 판단합니다.
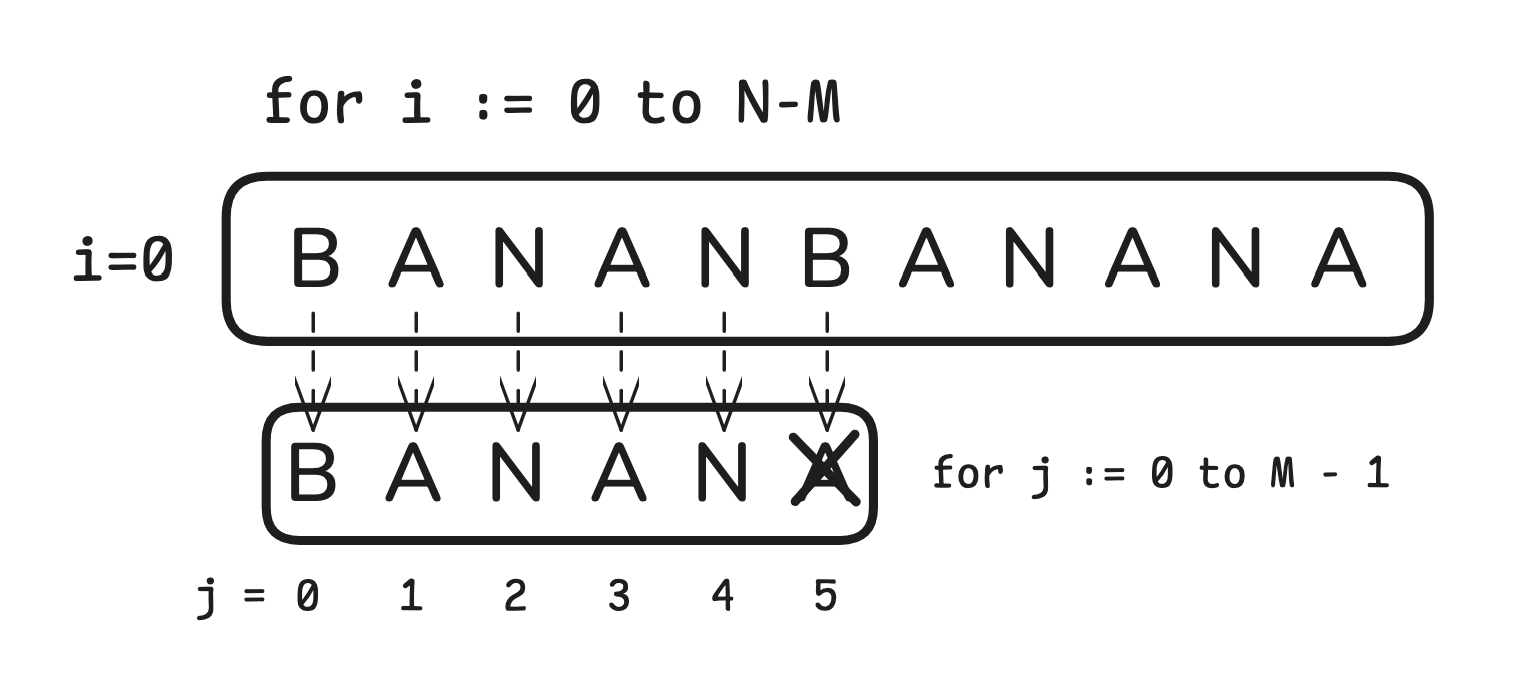
예를 들어 $i=0, j=5$ 일 때,
$T_{i+j}$와 $P_j$에 해당하는 문자가 일치하지 않기 때문에 $i=1$ iteration으로 넘어가게 됩니다.
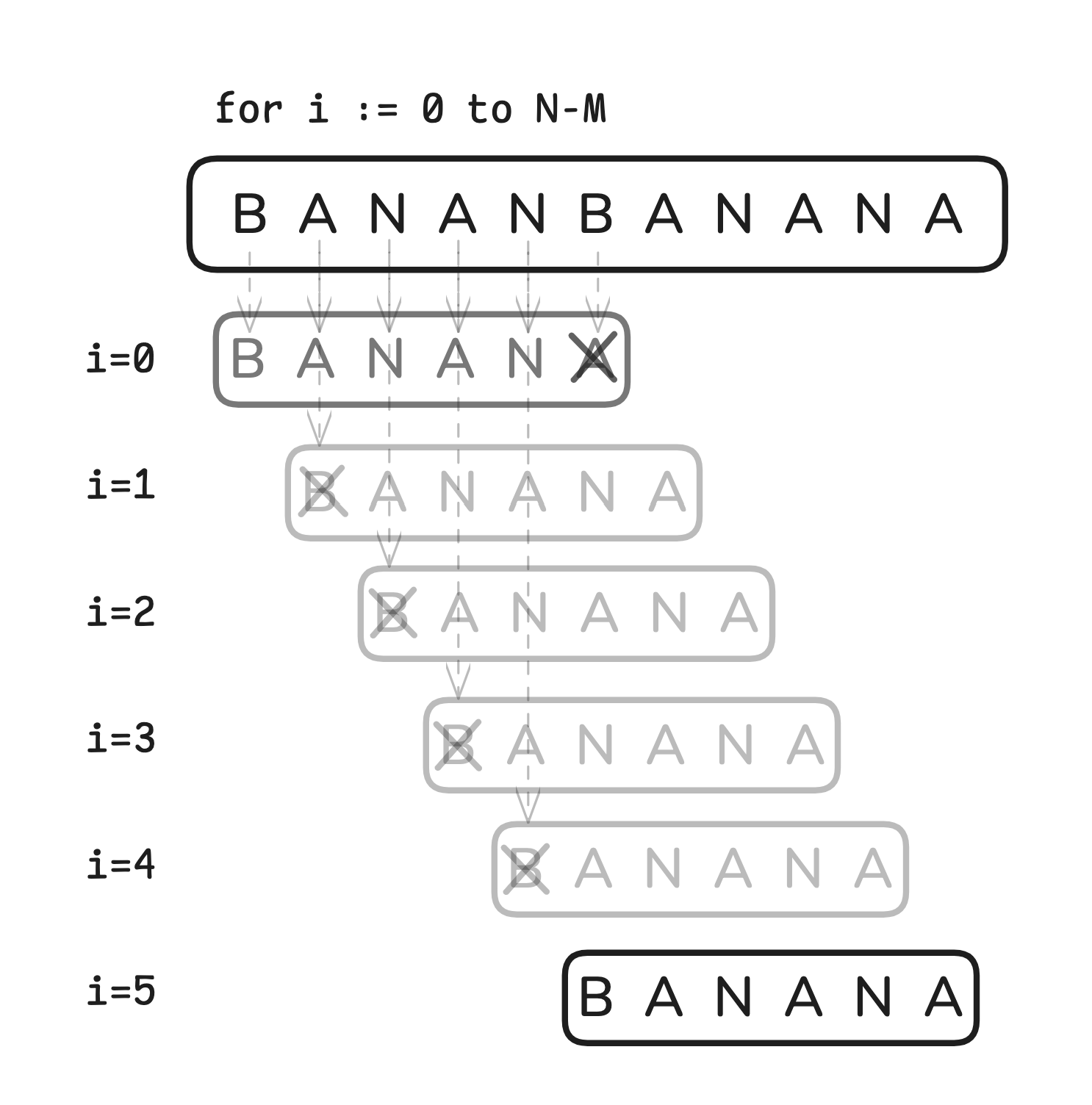
이렇게 naiveSearch() 함수는 텍스트에 대해서 $\Theta (N)$, 패턴의 모든 문자가 일치할 때까지 $\Theta (M)$에 대한 iteration을 수행합니다. 텍스트의 모든 문자가 패턴과 동일할 경우는 흔치 않으므로 평균적으로 $\Theta (N + M)$ 시간복잡도로 문제를 해결할 수 있는 올바른 알고리즘이라고 할 수 있죠.
우리는 Naïve 할 수 없다
모든 상황에 대해서 $\Theta (N + M)$의 시간복잡도로 문제를 해결할 수 있다면 해당 알고리즘은 좋은 선택지가 될 것 입니다. 하지만 Naïve Search 알고리즘은 그렇지 못하죠.
# 알고리즘에서 "평균적으로"라는 말이 의미하는 것은?
컴퓨터 공학, 특히 알고리즘에서 평균적으로 라는 말이 나온다는 것은 수행과정에서 무작위성의 절차 (probabilistic or randomized)가 존재하거나 입력에 대해 민감하다 (sensitive)는 것을 의미합니다.
즉, 사용함에 있어 어느정도의 성능을 기대할 수 있지만 구조상 성능을 기대하기 힘든 Worst-case가 존재한다는 것이죠.
저희가 자주 사용하는 Hash형 자료구조가 가장 대표적인 사례입니다.
각 연산에 대해 평균적으로 $O(1)$을 기대할 수 있지만, 조회 및 삽입 과정에서 의도적인 해시 충돌 (collision)을 일으켜 $O(N)$의 시간복잡도인 Worst-case가 발생하도록 유도할 수 있죠.
실제로 백준, 코드포스와 같은 알고리즘 문제 풀이 서비스에서 종종 볼 수 있는 문제입니다.
해당 포스트를 읽어보신다면 어떻게 Hash 함수를 저격 (hack)한다는 것인지 알 수 있을 것입니다.
어떤 상황이 문제가 될까요?
다음과 같은 문자열이 주어졌다고 해봅시다.
- $T$ : $aaaaaaaaaab$
- $P$ : $aaab$
- $\Sigma$ : $\{a, b\}$

이 상황에서 Naïve Search 알고리즘은 텍스트의 모든 문자열마다 패턴과 일치하는 지 판별하게 됩니다. 즉, $\Theta (N\cdot M)$의 시간복잡도로 해결할 수 밖에 없는 Worst-case라는 것이죠.
그렇다면 이런 질문을 할 수 있겠죠.
- Naïve Search 알고리즘은 잘못된 알고리즘일까?
- 실제 환경에서 이러한 문제가 자주 발생할까?
- 알고리즘에 Worst-case가 존재한다는 것이 문제가 될까?
제 생각에 모든 질문의 답은 "No" 입니다.
그렇다면 왜 우리는 naive 하지 말아야 할까요?
Naïve Search 알고리즘은 올바른 답을 도출하는 알고리즘 입니다. 하지만 개선점이 존재한다는 것이죠. 실제 환경에서 이러한 문제가 발생하지 않도록 통재할 수 없다면 우연의 일치로, 혹은 취약점을 알고 있는 악성 사용자로 인해 문제가 발생할 수 있겠죠. 게다가 Naïve Search 알고리즘의 Worst-case는 다른 알고리즘의 Worst-case 와는 비교도 할 수 없이 빈번하게 발생할 수 있는 문제기 때문에 개선이 필요한 상황입니다.
마지막으로 우리가 naïve 할 수 없는 가장 핵심적인 이유는 모든 상황에서 $\Theta (N)$의 시간복잡도로 문제를 해결할 수 있는 최적의 알고리즘을 누군가가 이미 만들어놨다는 것이죠. 그것도 상당히 적은 비용으로요!
DFA (Deterministic Finite State Automaton)
앞선 Naïve Search 알고리즘에서의 개선점은 선형 시간 (Linear time)으로 문제를 해결할 수 있도록 backup 과정을 생략하는 것입니다.
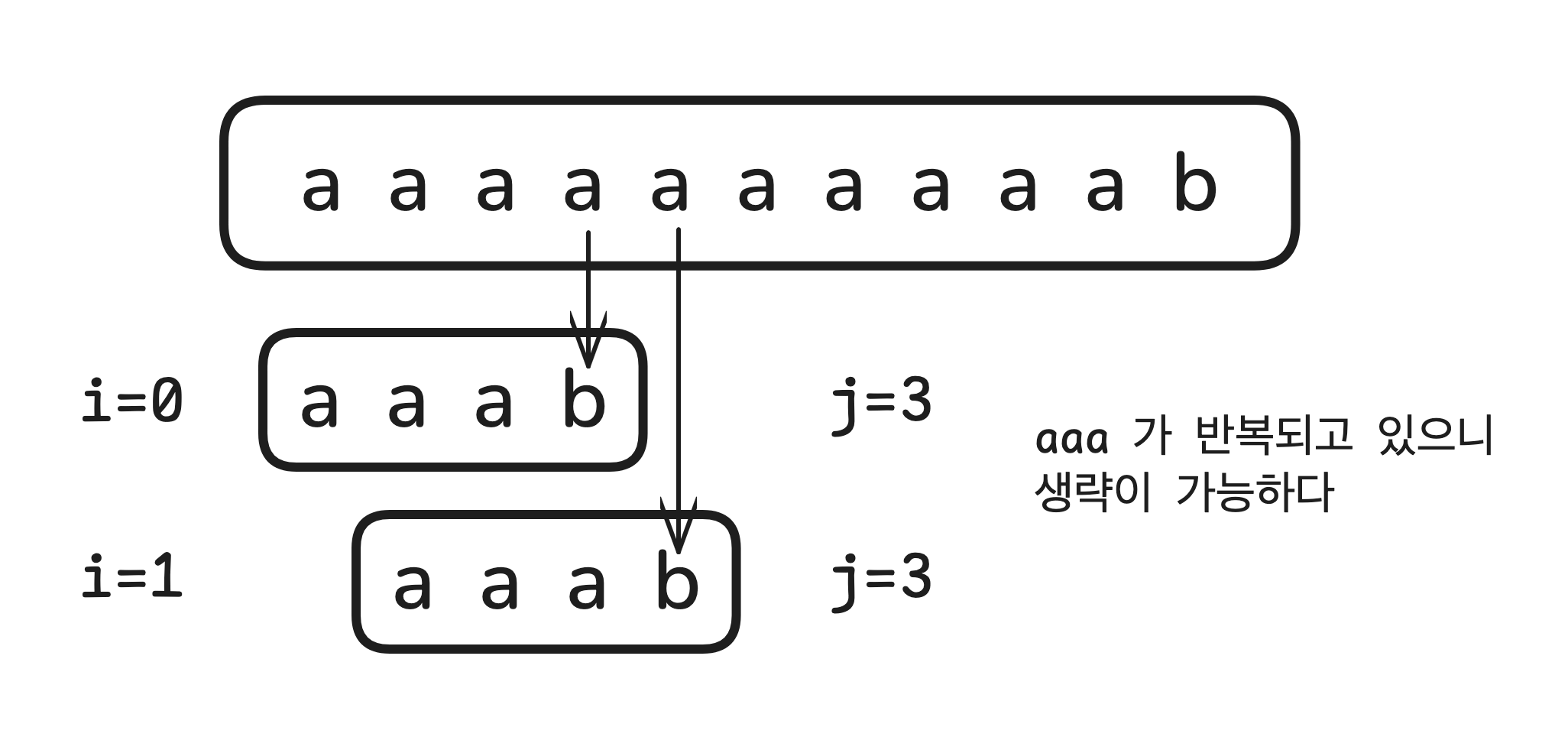
$i=0$ 일 때를 생각해봅시다.
$j=0$부터 $j=3$ 까지 비교하면서 $j=2$일 때까지 모든 문자일이 "일치"했습니다.
다음으로 $j=3$에서 텍스트와 패턴이 일치하지 않았죠. ($T_{i+j} \neq P_{j}$)
전체적인 매칭은 실패지만 현재까지 확인한 텍스트가 $aaaa$라는 중요한 사실을 알 수 있었습니다.
그렇다면 다음 과정은 무엇일까요?
$i=1, j=0$부터 $j=2$까지 이미 탐색한 문자열을 제외하고 (avoid backup) $i=1, j=3$부터 문자열을 비교하면 됩니다.
그렇게 $i=7, j=3$까지 비교하면서 정확히 11번 ($N$)의 비교만으로 $T$에 대한 모든 $P$의 등장 위치를 반별할 수 있게 되는 것이죠.
어떻게 이런 결과가 나올 수 있는 것일까요?
정답은 $T$를 이루는 모든 문자열($\Sigma$)이 각각의 비교하는 문자에 대한 유한한 상태를 갖기 때문입니다. (Exactly on transition for each char)
다시 말해, "지금 비교하는 텍스트의 알파벳이 무엇이냐"에 따라 다음에 비교할 알파벳이 정해진다는 것이죠.

텍스트에서 패턴 $aaab$의 첫 번째 문자 ($j=0$)를 비교해봅시다.
저희는 $a$를 제외한 그 어떤 문자도 필요하지 않죠. (첫 글자가 다른데 같은 단어일 수 없으니까요!)
만약, 지금 비교하는 문자가 $a$가 아니라면 ($T_{i+0} \neq P_0$) 텍스트의 다음 문자 ($T_{i+1}$)가 $a$인지 확인해보면 됩니다. 그리고 지금 확인한 문자가 $a$라면 ($T_{i+0} = P_0$) 첫 번째 문자가 일치한다는 것이니 두 번째 문자 (j=1)로 넘어가면 됩니다.

다음으로 패턴 $aaab$의 두 번째 문자 ($j=1$)를 비교해봅시다.
이전과 마찬가지로 저희에겐 지금 비교하는 문자 ($T_{i+1}$)가 $a$냐 아니냐만이 중요합니다. 비교하는 문자가 $a$라면 다음으로 넘어가 세 번째 문자와 비교를, 그렇지 않다면 다시 첫 번째 문자부터 비교하면 되기 때문입니다.

세 번째 문자를 비교하는 것도 이전과 동일하기 때문에 바로 네 번째 문자를 비교해보겠습니다.
네 번째 문자부터는 조금 달라지게 됩니다. 비교하는 문자와 패턴이 일치하는 문자가 바로 $b$기 때문이죠.
우선, 지금 비교하는 문자가 $a$와 $b$가 아니라면 ($T_{i+j} \notin \Sigma$) 저희는 다음부터 비교할 문자를 패턴의 첫 문자부터 비교하면 됩니다. 패턴에 포함되지 않는 문자가 존재하면 패턴과 일치할 수 없기 때문입니다.
다음으로 $a$일 때는 어떻게 될까요? 현재까지 확인한 텍스트가 $aaaa$라는 뜻이므로 다음에 비교할 텍스트 문자를 다시 패턴의 네 번째 문자와 비교하면 됩니다. 패턴의 첫 번째 문자부터 세 번째 문자까지 $aaa$를 만족하는 것은 동일하므로 처음부터 다시 비교할 필요가 없다는 것이죠.
그렇다면 비교하는 문자가 $b$라면 어떻게 될까요? 저희가 원하는 결과죠! 텍스트에서 지금까지 비교한 문자열이 패턴과 정확히 일치한다는 것이니 패턴의 등장 위치 ($i$)를 기억하고 계속해서 다음 문자를 비교하면 됩니다.

컴퓨터 공학에서 이러한 개념을 DFA (Deterministic finite automaton)라고 정의합니다.
각각의 state 마다 입력에 따른 유일한 상태 변화가 존재하기 때문에 다음과 같은 다이어그램으로 표현할 수 있다는 것이죠.
이제 실제 코드로 DFA searching을 확인해보겠습니다.
List<Integer> dfaSearch(String text, String pattern) {
int n = text.length();
int m = pattern.length();
List<Integer> matched = new ArrayList<>();
int state = 0;
for (int i = 0; i < n; i++) {
state = dfa[state][text.charAt(i)];
if (state == m) {
matched.add(i - m + 2);
state = dfa[state][pattern.charAt(m - 1)];
}
}
return matched;
}
dfaSearch() 함수는 state 변수를 통해 현재 상태를 관리합니다.
주어진 텍스트에 대한 iteration을 돌면서 현재 state를 사전에 계산한 dfa[][] 배열을 통해 비교하는 텍스트의 문자에 해당하는 state로 변경합니다. 변경을 하면서 state가 패턴과 완전히 일치하게 되면 (Accept state) 패턴의 등장 위치를 저장한 후 패턴의 마지막 문자에 해당하는 state로 이동하게 됩니다.
DFA를 활용한 문자열 검색 알고리즘 $\Theta (N)$의 시간복잡도로 텍스트에 등장하는 모든 패턴의 위치를 찾을 수 있는 빠르고 개선된 알고리즘 입니다. 결국, $\Sigma$에 해당하는 state 상태 변화를 사전에 계산한 후 이를 활용하는 메모이제이션의 응용이라고 볼 수 있는 것이죠.
DFA를 활용해 $\Theta (N)$의 시간복잡도로 문자열 검색 문제를 해결할 수 있다는 것은 매우 큰 강점이지만 한 가지 단점이 존재하죠.
문자열을 비교하기 전에 state 상태 변화를 계산하는 과정을 전처리 (preprocessing)라고 부릅니다.
DFA searching 알고리즘은 전처리 과정에서 패턴에 등장하는 모든 문자($\Sigma$)에 대해 계산하기 위해 $O(\vert\Sigma\vert\cdot M)$의 시간복잡도가 필요하며 state 정보를 저장하기 위한 $O(\vert\Sigma\vert\cdot M)$의 공간복잡도가 필요합니다.
# DFA preprocessing 함수 살펴보기 (Extended Ascii)
int[][] buildDFA(String pattern) {
int m = pattern.length();
int[][] dfa = new int[m + 1][256]; // ascii range
dfa[0][pattern.charAt(0)] = 1;
int x = 0;
for (int j = 1; j <= m; j++) {
System.arraycopy(dfa[x], 0, dfa[j], 0, 256);
if (j < m) {
dfa[j][pattern.charAt(j)] = j + 1;
x = dfa[x][pattern.charAt(j)];
}
}
// Transition for accept state
dfa[m][pattern.charAt(m - 1)] = x;
return dfa;
}
확장된 ascii 문자의 범위가 0부터 255라는 것을 생각하면 $\Sigma$는 256에 정도지만 범용적으로 사용하는 유니코드는 $2^{32}$ 정도로 저장하는 것은 불가능하며, 패턴의 길이 ($M$)가 10만 정도를 넘어간다면 전처리 과정에서 소요하는 시간과 배열의 크기가 상당히 커지기 때문에 일반적인 상황에서 가볍게 사용하기엔 적합하지 않다는 것입니다.
다시 말해 DFA string search 알고리즘에도 개선점이 존재한다는 것이죠.
KMP (Knuth-Morris-Pratt) algorithm
DFA string search 알고리즘의 문제는 전처리 과정에서 많은 시간이 소모 된다는 것 그리고 $\Sigma$에 해당하는 state 정보를 저장하기 위해 많은 공간이 필요하다는 것입니다.

이전 DFA 다이어그램을 보면 각 state 마다 비교하는 문자에 대한 모든 경우의 수 ($\Sigma$)를 정의했습니다. 그렇기 때문에 패턴에 있는 모든 문자마다 $\Sigma$에 해당하는 2차원 배열이 필요했던 것이죠.

각 state 마다 $\Sigma$에 해당하는 모든 경우의 수를 계산하는 것이 아닌 맞다, 틀리다에 대해서만 저장한다면 어떨까요? 위 다이어그램은 각 state에서 비교하는 텍스트의 문자와 패턴이 일치할 때 (1)와 불일치할 때 (0)에 대해서만 표현한 결과입니다. 그렇다면 이걸 배열로서 표현하면 어떨까요?
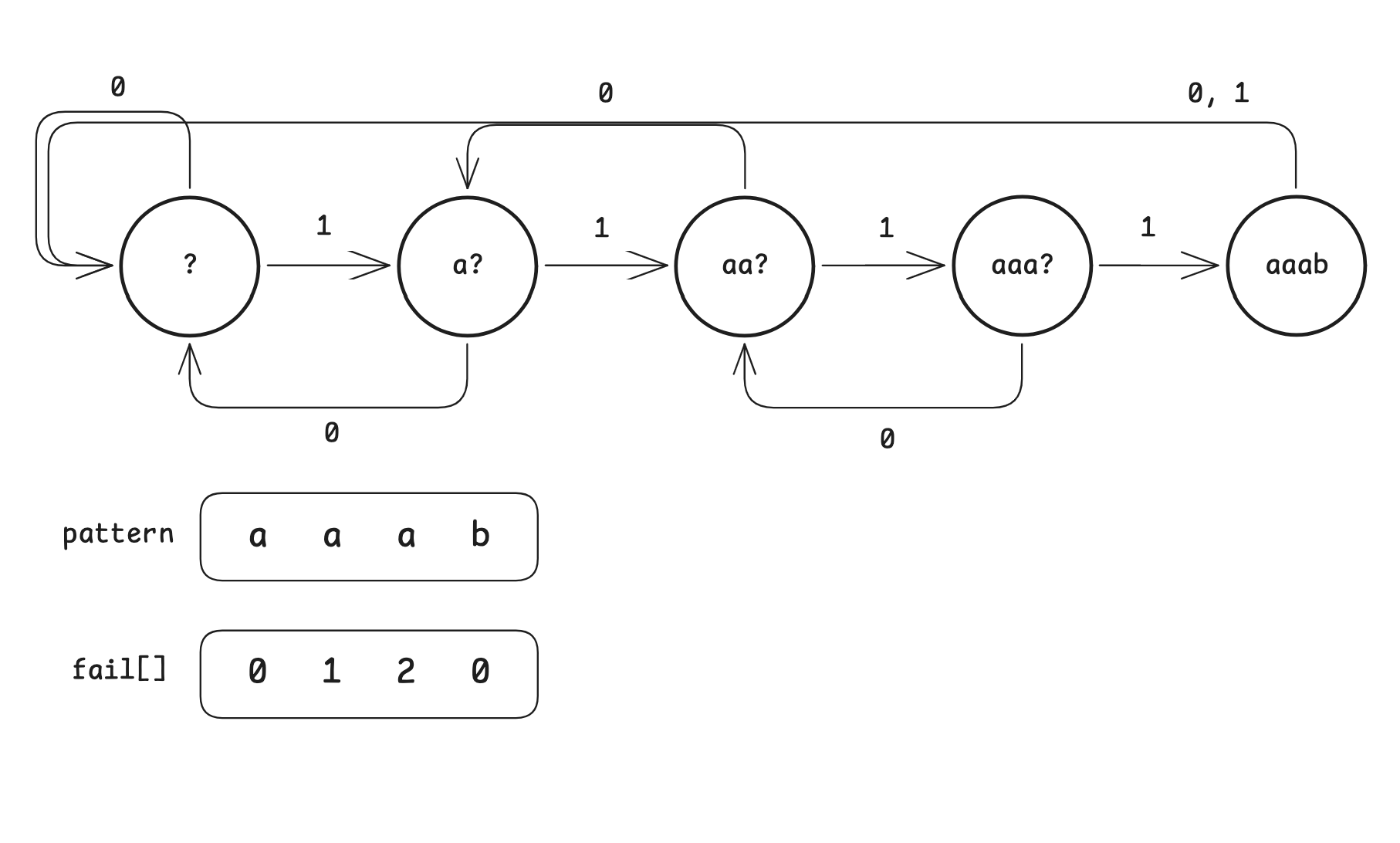
저희는 각 state에서 텍스트와 패턴을 비교해오면서 현재 state까지 모든 문자열이 일치한다는 사실을 알고 있습니다.
이러한 사실을 바탕으로 각 state에서 매칭에 실패했을 때 패턴의 몇 번째 문자부터 다시 비교를 하면 되는지 알 수 있는 것이죠
# KMP는 논문의 제목이 아니다! (A linear pattern-matching algorithm)
KMP 알고리즘은 이름에서 유추할 수 있듯이 Knuth, Morris, Pratt 세 명의 학자의 연구 결과로 1970년 A linear pattern-matching algorithm 이라는 Technical Report (TR-40)로 발표됐습니다.
KMP 알고리즘은 실패함수 ($pi$)를 사용해 불필요한 문자열 간의 비교를 생략하는 방식을 사용합니다.
본문에서 사용하는 fail[] 배열이 실패함수 ($pi$)로서의 기능을 한다고 생각해주시면 됩니다.
List<Integer> match(String text) {
List<Integer> matched = new ArrayList<>();
char[] t = text.toCharArray();
int j = 0;
for (int i = 0; i < t.length; i++) {
while (j > 0 && t[i] != p[j]) {
j = fails[j - 1];
}
if (t[i] != p[j]) {
continue;
}
if (j == p.length - 1) {
matched.add(i - j + 1);
j = fails[j];
} else {
j++;
}
}
return matched;
}
앞선 예제인 텍스트 $aaaaaaaaaab$, 패턴 $aaab$에 대해 KMP 알고리즘이 어떻게 동작하는지 알아보겠습니다

$i=0, j=3$ 일 때, 처음으로 텍스트와 패턴의 문자가 불일치하게 됩니다.
바로 그때 함수 내에 있는 while iteration을 거치게 되죠.
while 문에서 비교할 패턴의 문자에 해당하는 인덱스 $j$가 텍스트와 일치할 때까지 $j := fail[j - 1]$로 재할당됩니다.
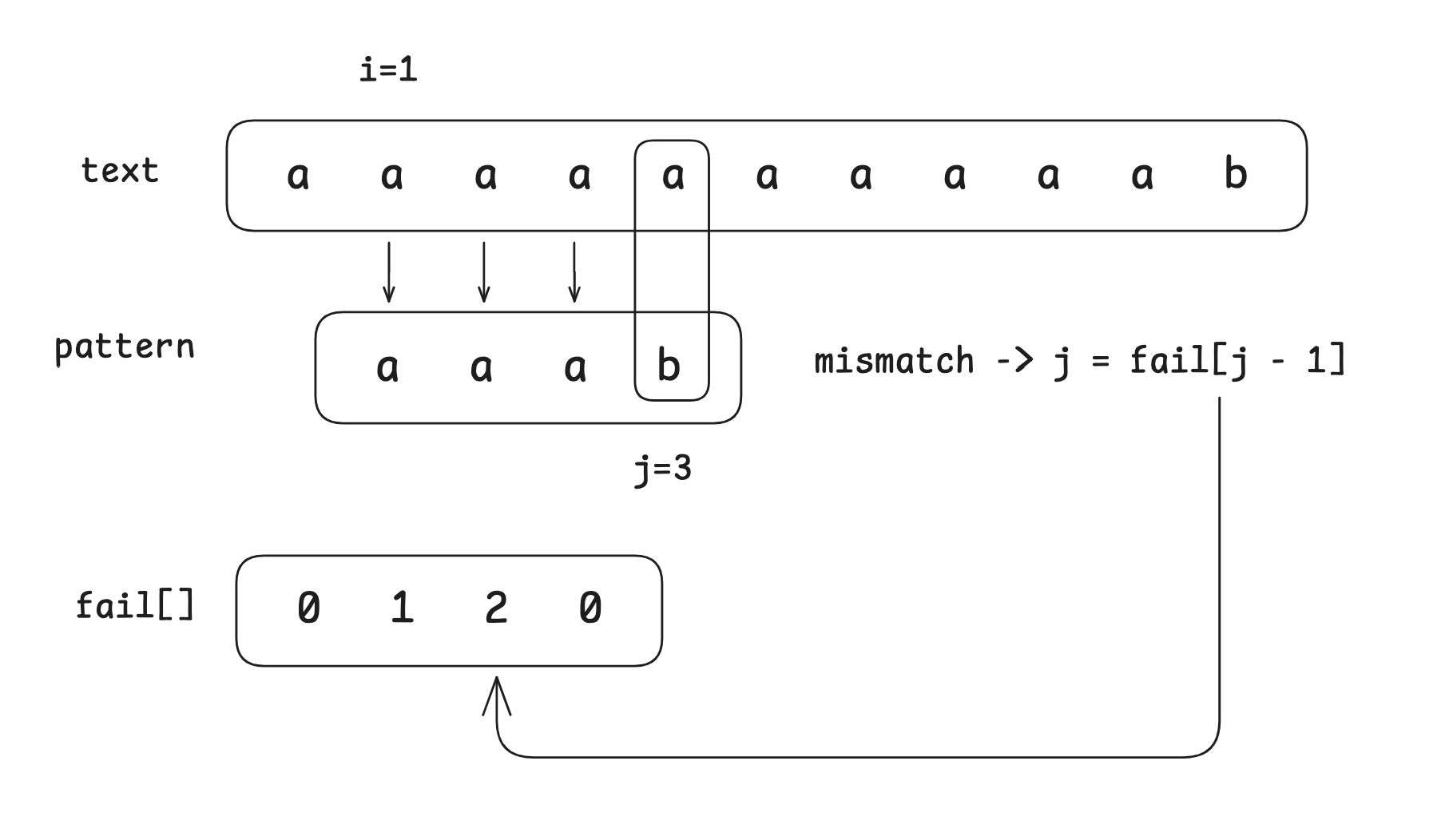
인덱스 $j$가 fail[] 배열을 통해 2로 재할당이 되지만 기존에 알고 있는 텍스트 $aaaa$가 패턴 $aaa$와 일치하기 때문에 $i=1, j=3$로 다시 비교를 시작하게 됩니다.

반복문을 거치고 거쳐 마지막 $i=7, j=4$까지 모든 패턴이 일치하는 상황이 됩니다.
이때 모든 반복문은 종료되게 되지만, $j$는 fail[j - 1]이 아닌 fail[j]로 할당이 되면서 반복문이 끝나지 않은 상황에서 패턴의 마지막 문자가 일치했을 때의 state (Transition for accept state)로 변경이 되는 것이죠.
결국, KMP 알고리즘의 핵심은 패턴에 대한 실패함수를 계산하는 것입니다.
이전 DFA 전처리 과정에서 $O(\vert\Sigma\vert\cdot M)$의 시간복잡도가 소요되었지만 KMP 알고리즘의 전처리 과정은 $\Theta (M)$의 시간복잡도를 필요로 합니다. 여기서 fail[] 배열을 계산하는 전처리 과정은 KMP 알고리즘 그 자체와 상당히 유사한 구조로 진행됩니다.
int[] getFail(String pattern) {
char[] p = pattern.toCharArray();
int[] fail = new int[p.length];
int j = 0;
for (int i = 1; i < p.length; i++) {
while (j > 0 && p[i] != p[j]) {
j = fail[j - 1];
}
if (p[i] == p[j]) {
j++;
}
fail[i] = j;
}
return fail;
}
fail[] 배열을 계산하는 과정은 패턴과 패턴 그 자체를 비교하는 과정이라고 볼 수 있습니다.
단, 동일한 두 패턴을 비교하는 것이 아닌 $\sum\limits_{i=1}^{M-1} P_i$와 $\sum\limits_{j=0}^{M-1} P_j$를 비교하면서 $P_i$에 대해 $j$를 fail[] 배열을 통해 변경하고 각 $state_i$에 대한 fail[i] 값을 계산하는 것이죠.
이렇게 DFA를 활용한 알고리즘에서 KMP 알고리즘을 사용하는 것을 통해 $\Theta (M)$의 시간복잡도와 공간복잡도로 전처리 과정을 단축할 수 있었고 저희가 궁극적으로 원했던 모든 텍스트와 패턴에 대해 다항 시간 $\Theta (N)$으로 문제를 해결할 수 있는 최적화된 알고리즘을 구현할 수 있었습니다.
이야기를 마치며
이번 이야기에서 간단한 방식의 Naïve 문자열 검색 알고리즘에서부터 Worst-case에 대한 소요 시간을 개선하기 위해 state를 활용하는 DFA, 그리고 전처리 과정의 소요 시간 및 공간적인 제약을 개선한 KMP 알고리즘까지 상당히 많은 볼륨을 다뤘습니다. 그 과정에서 메모이제이션에 대한 내용과 Hash형 자료구조에 대한 내용도 잠깐 언급되면서 다양한 컴퓨터 공학의 개념을 다룰 수 있어서 뿌듯한 감정도 드는 것 같습니다.
여담으로 문자열 검색은 이번에 살펴본 것 이상으로 다양한 알고리즘이 존재합니다.
| Alogorithm | Preprocessing time | Average time | Worst time |
| Naïve | 0 | $\Theta (n+m)$ | $\Theta (n\cdot m)$ |
| Rabin-Karp | $\Theta (m)$ | $\Theta (n)$ | $O(n\cdot m)$ |
| Deterministic Finite State Automaton | $O(m \cdot\vert\Sigma\vert)$ | $\Theta (n)$ | $\Theta (n)$ |
| Knuth-Morris-Pratt | $\Theta (m)$ | $\Theta (n)$ | $\Theta (n)$ |
| Two-way matching | $\Theta (m)$ | $O(n)$ | $\lceil O(\log m)\rceil$ |
궁금해하실 분들을 위해 간략하게 소개드리자면 Hashing을 사용하는 Rabin-Karp 알고리즘과 Java의 String.indexOf()에서 사용하는 Two-way matching 알고리즘도 중요한 문자열 검색 알고리즘 입니다. 각각의 알고리즘의 내부 구현 방식은 차이가 있지만 그 중에서도 가장 핵심이 되는 KMP 알고리즘을 이해한 여러분이라면 다른 알고리즘들도 큰 무리 없이 이해할 수 있을 것이라 생각합니다.
끝으로 이론적인 내용을 넘어서 직접 활용해보고 싶은 분도 계실 것 같은데요.
그런 분들께 백준 1786번 찾기 문제를 추천드립니다.
직접 Naïve, DFA, KMP를 구현해보면서 시간 초과, 메모리 초과, 성공으로 나아가는 과정을 느껴보신다면 더욱 깊이 있는 이해도를 갖추실거라 장담합니다.
여기까지가 문자열 검색 (String searching) 이야기였습니다.
이 글이 저를 포함한 모든 독자분들께 개발자로 성장하는 여정의 밑거름이자 나침반으로써 도움이 되었기를 바랍니다.
감사합니다.
