이야기에 앞서
이번 이야기는 메모이제이션 (Memoization) 입니다.
정확히 같은 뜻은 아니지만 편의상 더 넓은 개념인 동적계획법 (Dynamic Programming) 이라고도 부르죠.
동일한 문제를 반복적으로 계산해야 할 때
이전에 계산한 결과를 기억해 중복적인 계산 과정을 생략한다.
메모이제이션은 문제를 해결할 때 "이미 계산한 결과가 있으면 다시 계산하지 않는다"라는 간단한 개념에서부터 시작합니다. 정말 단순한 내용이지만 정확히 어떤 상황에서 사용할 수 있는 개념인지 그리고 어떤 방법으로 계산된 결과를 저장할 수 있는지는 말로만 듣고 이해하기란 쉬운 일이 아니죠.
그래서 이번 이야기에서는 백준 1520번 문제 내리막 길을 직접 풀어보면서 메모이제이션에 대한 전반적인 개념을 이해하고 코드로서 표현해보도록 하겠습니다.

문제 상황
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
...중략...
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
- 백준 1520번 내리막길 중 -
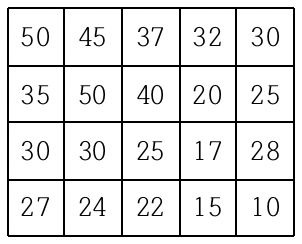
세준이가 지도를 갖고 있습니다.
지도의 좌측 상단 (1, 1)에서 출발해서 우측 하단 (4, 5)로 이동할 수 있는 모든 경로의 수를 알고 싶다고 하군요.
이때 상하좌우 어디로든 갈 수 있지만 현재 타일에 적혀있는 숫자보다 작은 타일로만 이동할 수 있다고 합니다.
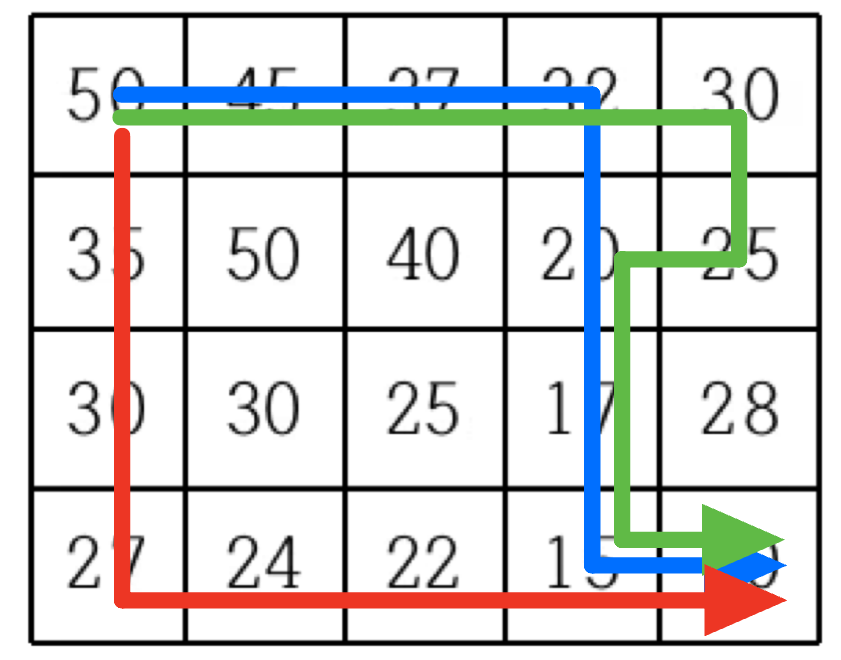
해당 지도에서는 총 3가지 경로가 존재하네요.
빨간색, 파란색, 초록색 경로를 따라 이동한다면 상하좌우
그리고 내리막 길로 이동한다는 규칙을 만족하면서 목적지로 도착할 수 있습니다.
그렇다면 이렇게 모든 경로의 수를 구하기 위해선 어떻게 해야 할까요?
이렇게 표현해 볼까요?
각각의 경로가 타일을 하나하나 거쳐온 길을 보면 특정 부분 (분기점) 에서 갈라지고 다시 모이게 되는데요.
경로가 그려진 그림을 보면 뭔가 새로운 정보를 도출해 낼 수 있을 것 같습니다.
한 번 각 경로가 지나오는 경로에 숫자를 표기해 보겠습니다.
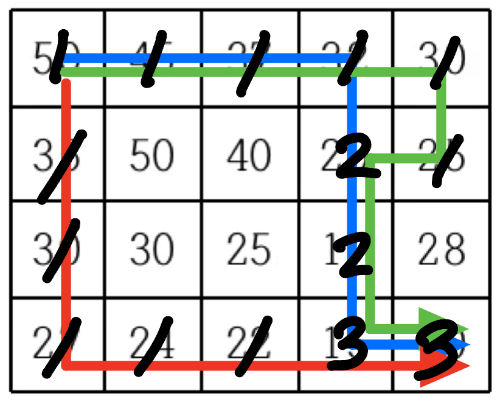
각 경로의 분기점에서 해답에 대한 실마리가 보이기 시작합니다.
결국 목적지로 갈 수 있는 모든 경로의 수는 목적지 타일로 갈 수 있는 타일들의 경로의 합과 같습니다.
그런데 이게 왜 메모이제이션이라는 걸까요? 그냥 평범한 그래프 탐색 문제로 보이지 않나요?
왜 메모이제이션인가?
규칙을 찾으면서 이게 왜 메모이제이션일까? 이해하지 못하는 분도 계실 것 같습니다.
그 이유는 단순합니다. 저희가 아직 문제를 해결하기 위해 어떠한 접근도 하지 않았기 때문이죠.
문제를 풀기 위해 이렇게 접근해 보겠습니다. 다음과 같은 함수가 있다고 생각해보죠.
class Main {
// 중략
public static void main(String[] args) throws IOException {
init(); // padding을 통해 (1, 1) -> (n, m)에 도착하도록 구성
System.out.println(travel(n, m));
}
private static int travel(int r, int c) {
if (r == 1 && c == 1) {
return 1;
}
int path = 0;
if (map[r][c] < map[r + 1][c]) {
path += travel(r + 1, c);
}
if (map[r][c] < map[r - 1][c]) {
path += travel(r - 1, c);
}
if (map[r][c] < map[r][c + 1]) {
path += travel(r, c + 1);
}
if (map[r][c] < map[r][c - 1]) {
path += travel(r, c - 1);
}
return path;
}
}
도착지 (n, m)에서 출발해서 인접한 타일 중 올라갈 수 있는 다음 타일로 이동한 후 재귀적으로 다음 타일의 값을 호출합니다. 올라갈 수 있는 타일로 이동하면 탈출 조건인 출발지 (1, 1)에서 1을 반환하기 때문에 결과적으로 출발지에서 도착지까지 갈 수 있는 모든 경로의 수를 반환하게 됩니다.
올바른 답을 도출할 수 있는 방법이네요! 하지만 효율적이라고 할 수 있을까요?

그림을 보면 파란색 경로 찾기 위해 32번 타일 (1, 4)의 값을 미리 계산한 상황입니다.
이 과정에서 32번 타일 (1, 4) 이 1을 반환한다는 것을 알 수 있죠.
하지만 초록색 경로를 찾아가는 과정에서 또다시 32번 타일의 값을 계산하게 됩니다.
해당 코드에는 한 가지 개선점이 존재합니다.
바로 각 타일로 이동하는 경로의 수를 구하는 과정에서 동일한 문제를 반복적으로 계산한다는 것이죠.
바로 이 부분에서 왜 메모이제이션을 사용해야 하는지 알 수 있습니다.
지금과 같이 목적지부터 출발지까지 경로를 계산하는 하향식(Top-Down)으로 문제를 해결한다면 메모이제이션을 통해 반복적인 계산 과정을 생략하고 보다 효율적으로 문제를 해결할 수 있다는 것이죠.
메모이제이션을 사용해 코드를 개선해 보자
코드를 어떻게 개선할 수 있을까요?
travel(int r, int c) 함수는 좌표를 기준으로 각 타일의 값을 계산하기 때문에 계산된 값을 저장하기 위해 파라미터로 전달받은 좌표를 활용할 수 있을 것 같습니다.
그렇다면 2차원 배열 (int[][]) 이나 해시형 자료 구조 (Map<Point, Integer>) 를 사용해 계산된 정보를 저장한다면 어떨까요?
class Main {
// 중략
private static int travel(int r, int c) {
if (map[r][c] != -1) {
return memo[r][c];
}
memo[r][c] = 0;
update(r, c, r + 1, c);
update(r, c, r - 1, c);
update(r, c, r, c + 1);
update(r, c, r, c - 1);
return memo[r][c];
}
private static void update(int r, int c, int tr, int tc) {
if (map[r][c] < map[tr][tc]) {
map[r][c] += travel(tr, tc);
}
}
}
travel(int r, int c) 함수는 더 이상 반복적인 계산이 필요하지 않습니다.
memo[][]라는 2차원 배열에 이전에 계산한 결과가 있다면 early return을 통해 저장된 값을 반환합니다. 그렇지 않다면 update(int r, int c, int tr, int tc) 함수를 상하좌우 4번 호출하면서 재귀적으로 타일에 도달할 수 있는 경로의 수를 계산하죠.
최종적으로 좌표 (r, c)에 해당하는 타일의 값을 memo[][] 배열에 저장하고 반환하면서 계산한 값을 기억하고 활용할 수 있는 똑똑한 함수로 개선되었습니다.
입출력 및 패딩 과정을 포함한 전체 소스 코드는 해당 링크에서 확인하실 수 있습니다.
글을 마치며
이로써 메모이제이션이 무엇인지 그리고 어떤 문제 상황에서 활용할 수 있는지 모두 알아보았습니다.
사실 메모이제이션은 정말 다양한 문제에서 활용할 수 있는 개념입니다. 본문에서 다룬 케이스는 정말 단순한 문제 상황에 불과하죠.
"수학적인 점화식이 존재하는 문제에서 메모리에 값을 저장하는 것이 메모이제이션이다"라고 생각할 수 있지만, 백엔드 아키텍처에서 반복적인 API 호출 과정 중 cache를 활용해 소비자에게 쾌적한 서비스를 제공하는 것도 어떤 의미에서는 메모이제이션이라고 할 수 있겠죠. 결국, 문제를 해결하기 위해 소프트웨어를 설계하는 과정에서 State를 활용하는 것이 하나의 해결 방법이 될 수 있다는 것입니다.
여기까지가 메모이제이션 이야기였습니다.
이 글이 저를 포함한 모든 독자분들께 개발자로 성장하는 여정의 밑거름이자 나침반으로써 도움이 되었기를 바랍니다.
감사합니다.
